Evolves the Field according to the Time-Dependent Gross-Pitaevskii (TDGP) Equation (this is the 2D version).
The Gross-Pitaevskii Equation in the following form is used
![\[ \left[1 - \frac{i\hbar\Delta t}{4m}\frac{\delta^2_{x}}{\Delta x^2} - \frac{i\hbar\Delta t}{4m}\frac{\delta^2_{y}}{\Delta y^2}\right]\Psi^{n+1} = \left[1 + \frac{i\hbar\Delta t}{4m}\frac{\delta^2_{x}}{\Delta x^2} + \frac{i\hbar\Delta t}{4m}\frac{\delta^2_{y}}{\Delta y^2}\right]\Psi^{n} + \frac{\Delta t}{2}\left[f^{n+1} + f^n\right] \]](form_0.png)
where
![\[ f^{n+1} = \frac{\Delta t}{2i\hbar}m\omega^2(x^2 + y^2)\Psi^{n+1}_{k,\ell} + \frac{\Delta t}{2i\hbar}g|\Psi^{n+1}_{k,\ell}|^2\Psi^{n+1}_{k,\ell} \]](form_1.png)
This is approximately factorized to give the first fractional timestep as
![\[ A_{x}\Psi^{n+1/2} = B_x B_y\Psi^{n} + \frac{\Delta t}{2}\left[f^{n+1} + f^n\right] \]](form_2.png)
and the second fractional timestep is
![\[ A_{y}\Psi^{n+1} = \Psi^{n+1/2} \]](form_3.png)
where each of the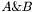 
are tridiagonals to be solved It is assumed that Small Omega Squared is 1st Parameter, mu is the 2nd, g is 3rd Parameter and hbar the 4th Parameter, m the 5th, Big Omega the 6th and the Winding number of the vortex has the 7th in the QCParameter Class. All index referencing should be made C style.
- Todo:
- Generalise the evolving algorithms for multiple dimensions
Definition at line 54 of file qcevolve.cpp.
References QCField< complexType, rank >::accessArray(), QCParameter::getParameter(), QCField< complexType, rank >::noOfColumns(), QCField< complexType, rank >::noOfRows(), and QCField< complexType, rank >::retrieveElement().
Referenced by QCBEC< rank >::evolve().
![\[ \frac{\Omega}{2}\left[x\frac{\delta_{y}\Psi^{n+1}}{\Delta y} - y\frac{\delta_{x}\Psi^{n+1}}{\Delta x}\right] \]](form_5.png)
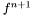. It is assumed that Small Omega Squared is 1st Parameter, mu is the 2nd, g is 3rd Parameter and hbar the 4th Parameter, m the 5th, Big Omega the 6th and the Winding number of the vortex has the 7th in the 